What is sorting?
Sorting means to arrange elements of a collection in an order which can be either ascending or descending. Collection can be an array, a list, keys or values of a map etc. Usually when sorting techniques are discussed, the collection is sorted in ascending order of its elements and the collection picked up is an array.
There are many approaches available to sort an array. This post will focus on Bubble sort.
What is Bubble sort?
It is a sorting algorithm in which each array element is compared with the element next to it. If the element being compared is greater than the element next to it, they are swapped(their positions are interchanged).
Multiple iterations of the array are performed and each iteration starts with the first array element and ends till the whole array is completed. At the end of each iteration, the greatest element moves(or bubbles up) to the right end, hence its name Bubble sort.
Total iterations in Bubble sort are equal to Number of array elements – 1. (though this can be reduced as explained later)
Bubble sort algorithm
Following steps constitute the algorithm for bubble sort.
- Compare first element with second. Swap them if first element is greater than second else do nothing.
- Compare second element with third, third with fourth and so on till the last element is reached. Keep on swapping elements if the they are in reverse order.
- Above steps 1 and 2 are called one iteration. After each iteration, the largest element moves to the
rightmost end of the array. - Repeat iterations till whole array has been traversed.
- After all iterations are complete, the array will be sorted. In worst case, the number of iterations will
be equal to the total elements – 1.
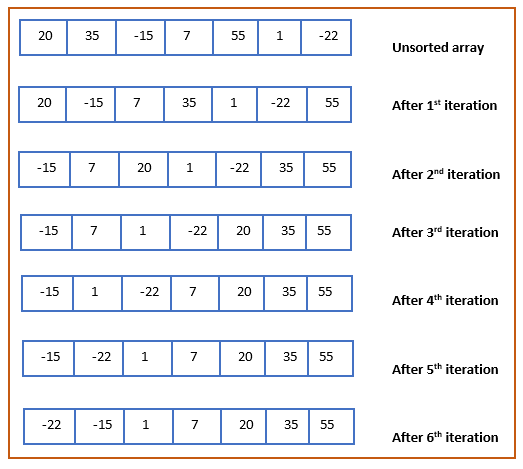
Consider an array with elements 20, 35, -15, 7, 55, 1, -22. In order to sort it in ascending order using Bubble sort, multiple iterations are performed. Following are the detailed steps performed in every iteration.
- Compare first element with second, that is, 20 with 35. Since it is less than 35, do nothing.
- Compare second element with third, that is, 35 with -15. Since 35 is greater than the element next to it, swap them.
- Compare third element with fourth, that is 35 with 7. Since 35 is greater than the element next to it, swap them. Note that 35 was swapped in last step so it became the third element.
- Compare fourth element with fifth, that is 35 with 55. Since 35 is less than the element next to it, no swapping is done. Note that 35 was swapped in last step so it became the fourth element.
- Compare fifth element with sixth, that is 55 with 1. Since 55 is greater than the element next to it, swap them.
- Compare sixth element with seventh, that is 55 with -22. Since 55 is greater than the element next to it, swap them. Note that 55 was swapped in last step so it became the third element.
All the array elements are traversed and this ends the First iteration. Note that after first iteration, the greatest array element is positioned at the right most end(or it bubbled up the array).
Again when Second iteration starts, all the above steps are repeated. This continues till the number of iterations are equal to the total array elements – 1 or the array is sorted.
Below illustration will clarify the concept of bubble sort and position of elements after every iteration.
Bubble sort program in java
Above algorithm can be translated into a java program as given below.
public class BubbleSort {
public static void main(String[] args) {
int[] arr = { 20, 35, -15, 7, 55, 1, -22 };
System.out.println("Array before sorting");
printArray(arr);
System.out.println("-------------------------");
bubbleSort(arr);
System.out.println("-------------------------");
System.out.println("Array after sorting");
printArray(arr);
}
static void bubbleSort(int[] arr) {
int length = arr.length;
// iterate over array
for (int i = 0; i < length - 1; i++) {
// iterate till the last sorted element
for (int j = 0; j < length - i - 1; j++) {
// check if the current element is greater
// than the next one
if (arr[j] > arr[j + 1]) {
// swap elements
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
// print array state after this iteration
System.out.println("After " + "iteration " + (i + 1));
printArray(arr);
}
}
static void printArray(int[] arr) {
// iterate over array and print its elements
for (int i = 0; i < arr.length; i++) {
int j = arr[i];
System.out.print(j + " ");
}
System.out.println();
}
}
Method bubbleSort contains two nested loops. Outer loop iterates over the array starting from the first to last element. Inner loop iterates over the array starting from the first element till the last sorted element.
It compares the current array element with its next element and swaps them if current element is greater than the next.
In relation to the above explained algorithm, the inner loop represents one iteration.
Thus after each complete execution of inner loop, the highest element is placed at the rightmost end of the array and after the outer loop completes the array will be sorted in ascending order of elements.
This way smallest element will move towards right.
Output of above code execution will be
Array before sorting
20 35 -15 7 55 1 -22
————————-
After iteration 1
20 -15 7 35 1 -22 55
After iteration 2
-15 7 20 1 -22 35 55
After iteration 3
-15 7 1 -22 20 35 55
After iteration 4
-15 1 -22 7 20 35 55
After iteration 5
-15 -22 1 7 20 35 55
After iteration 6
-22 -15 1 7 20 35 55
————————-
Array after sorting
-22 -15 1 7 20 35 55
Notice that the total number of iterations is equal to array elements – 1(7-1) and after all the iterations the array is sorted in ascending order of elements.
[AdSense-A]Optimization
For some array elements, it might happen that the array becomes sorted after a few iterations only(that is, after a few executions of inner loop) and it is not necessary to iterate over the array after that.
Consider the array with elements 8, 1, 99, -34, 87, 10, 22. When above code is executed using this array, the output is
Array before sorting
8 1 99 -34 87 10 22
————————-
After iteration 1
1 8 -34 87 10 22 99
After iteration 2
1 -34 8 10 22 87 99
After iteration 3
-34 1 8 10 22 87 99
After iteration 4
-34 1 8 10 22 87 99
After iteration 5
-34 1 8 10 22 87 99
After iteration 6
-34 1 8 10 22 87 99
————————-
Array after sorting
-34 1 8 10 22 87 99
You can see that the array has been completely sorted after third iteration only. Rest all iterations are unnecessary. This is because the algorithm/code has no way of to determine if the array is already sorted.
Thus, if we could determine that the array is sorted, further iterations can be prevented. Given below is the optimized version of the above code which avoids unnecessary iterations.
public class BubbleSort {
public static void main(String[] args) {
// int[] arr = { 20, 35, -15, 7, 55, 1, -22 };
System.out.println("Array before sorting");
printArray(arr);
System.out.println("-------------------------");
bubbleSort(arr);
System.out.println("-------------------------");
System.out.println("Array after sorting");
printArray(arr);
}
static void bubbleSort(int[] arr) {
int length = arr.length;
// iterate over array
for (int i = 0; i < length - 1; i++) {
// flag to check if any elements were swapped in this iteration
boolean isSwapped = false;
// iterate till the last sorted element
for (int j = 0; j < length - i - 1; j++) {
// check if the current element is
// greater than the next one
if (arr[j] > arr[j + 1]) {
// swap elements
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
// mark the flag to indicate swapping of elements
isSwapped = true;
}
}
// terminate loop if there no swappings
if (!isSwapped) {
break;
}
// print array state after this iteration
System.out.println("After " + "iteration " + (i + 1));
printArray(arr);
}
}
static void printArray(int[] arr) {
// iterate over array and print its elements
for (int i = 0; i < arr.length; i++) {
int j = arr[i];
System.out.print(j + " ");
}
System.out.println();
}
}
This code takes a boolean variable which is set to false at the start of outer loop iteration. When ever two elements are swapped, this variable is set to true indicating that some elements were found in unsorted stated in the array.
After the inner loop completes(when one complete iteration of array has been done), this boolean variable is checked.
If it is false, this means that no elements were swapped in this iteration, which indicates that the array is in sorted state and no more iterations are required and outer loop is terminated. This prevents unnecessary iterations.
When the above program is again executed, the output is
Array before sorting
8 1 99 -34 87 10 22
————————-
After iteration 1
1 8 -34 87 10 22 99
After iteration 2
1 -34 8 10 22 87 99
After iteration 3
-34 1 8 10 22 87 99
————————-
Array after sorting
-34 1 8 10 22 87 99
See we have saved 3 iterations.
Bubble sort complexity
Bubble sort is not the most efficient sorting algorithm and it takes 100 steps to sort 10 elements, 10, 000 steps to sort 100 items and so on. Its complexity goes on increasing as the number of elements to be sorted increases. Its complexity metrics are:
Worst Case: This is the case when the array is sorted in reverse order, that is, greatest element is at first place and smallest element is last. Its time complexity is O(n2).
Average Case: This is the case when the array is moderately sorted, that is, elements are evenly distributed across the array. Time complexity in this case is also O(n2).
Best Case: This occurs when the array is already sorted. Its time complexity in this case will be O(n).
Hope this post helped you in understanding how bubble sort works and how to implement it in java. Keep visiting for more such stuff.