Java bubble sort

Bubble sort in java
In bubble sort algorithm, each array element is compared with the element ahead of it. Elements are swapped if the element ahead(or right element) is smaller than the left element(in case the array needs to be sorted in ascending order).
This article will explain how to sort an array using bubble sort, along with program example in java.

Logic
Consider that we have an unsorted array as shown below and it needs to be sorted in ascending order.

 

 

 

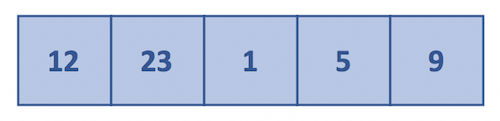
Bubble sort logic involves the following steps to be followed.
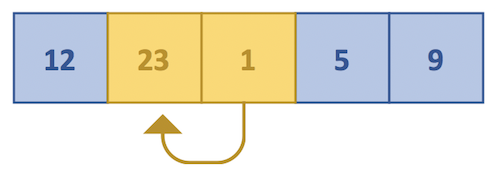
1. Start with the first element(12) and compare it with the second element(23).
If the second element is lesser than the first, both are swapped or interchanged.
2. Next, compare the second and third elements. Swap them, if the third element is greater than the second, as shown below.

 

 

 

 

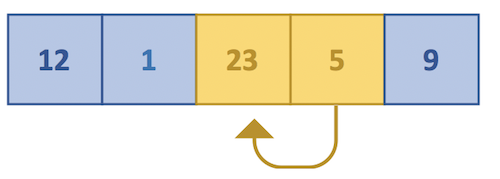
3. Continue with the third and fourth elements as shown below.

 

 

 

 

 

4. And finally with fourth and fifth elements as below.

 

 

 

 

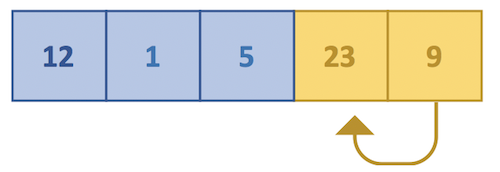
This is called the first pass or the first iteration of the loop.
You can see that after the first pass, the largest element bubbles up to the top. Hence, this type of sorting is called Bubble sort.
In subsequent passes, the second, third, and corresponding elements bubble towards the end of array. When all the passes are complete, the array becomes sorted.

Algorithm
1. Loop over the array from 0 to the last element.
2. Start another loop from 1 till the last element for comparing each element with the element ahead it. This loop represents the pass that was explained above.
Thus, one complete execution of the loop is one pass and after each pass the next largest element moves towards the end of the array.
3. Inside the loop in step 2, compare each element with the next element and interchange both if the next element is lesser than the previous. This is required if we need to sort the array in ascending order. For descending order, the elements will be exchanged if the next element is greater than the previous.
4. After the loop in Step 1 completes, the array will be sorted.
Implementation
Below is a java code to implement the pseudocode explained above.

public class BubbleSortExample {

  public static void main(String[] args) {
    int[] arr = { 12, 23, 1, 5, 9 };
    System.out.println("Before sorting: " + Arrays.toString(arr));
    for (int i = 0; i < arr.length; i++) {
      for (int j = 1; j < arr.length; j++) {
        if (arr[j] < arr[j - 1]) {
          int temp = arr[j];
          arr[j] = arr[j - 1];
          arr[j - 1] = temp;
        }
      }
    }
    System.out.println("After sorting: " + Arrays.toString(arr));
  }
}

This prints

As you can see from the output, the array is sorted in ascending order.

Sorting string array
Bubble sort can also be used to sort an array of string values. The only difference is that string values can not be compared using logical operator(>).
We need to use compareTo() method for checking if one string is greater than other.
compareTo() is invoked on a string and it accepts another string as argument. It compares the strings alphabetically and returns an integer value as per the following conditions:

• Negative value or <0 , if the string on which it is called is lesser than the argument string.
  Example,  "ab".compareTo("cd");
• Positive value or >0 , if the string on which it is called is greater than the argument string.
  Example,  "xy".compareTo("cd");
• 0 , if both the strings are equal.
  Example,  "ab".compareTo("ab");

Java program to sort a string array based on insertion sort is given below.

public class BubbleSortExample {

  public static void main(String[] args) throws IOException {
    String[] arr = { "owl", "cat", "apple", "ball", "east" };
    System.out.println("Before sorting: " + Arrays.toString(arr));
    for (int i = 0; i < arr.length; i++) {
      for (int j = 1; j < arr.length; j++) {
        if (arr[j].compareTo(arr[j - 1]) < 0) {
          String temp = arr[j];
          arr[j] = arr[j - 1];
          arr[j - 1] = temp;
        }
      }
    }
    System.out.println("After sorting: " + Arrays.toString(arr));
  }
}

Output of this code is

String array is successfully sorted.
Time complexity
Following is the time complexity of bubble sort.
Best Case
Best case is when the array is already sorted in the order you wish. In this case, we need to iterate all the array elements[O(n)] but no swapping or shifting of elements is required[O(1)].
So, the time complexity is O(n).

Worst Case
Worst case is when the array is sorted in the reverse order than you wish. In this case, we need to iterate all the array elements[O(n)] and perform (n-1) comparisons to swap or shift elements[O(n)].
So, the time complexity is n(n – 1) ~ O(n²).

Average Case
Worst case is when the array is not sorted in any order and the elements are randomly distributed. In this case, we need to iterate all the array elements[O(n)] and swap or shift elements[O(n)].
So, the time complexity is O(n²).

Hope this article was useful.